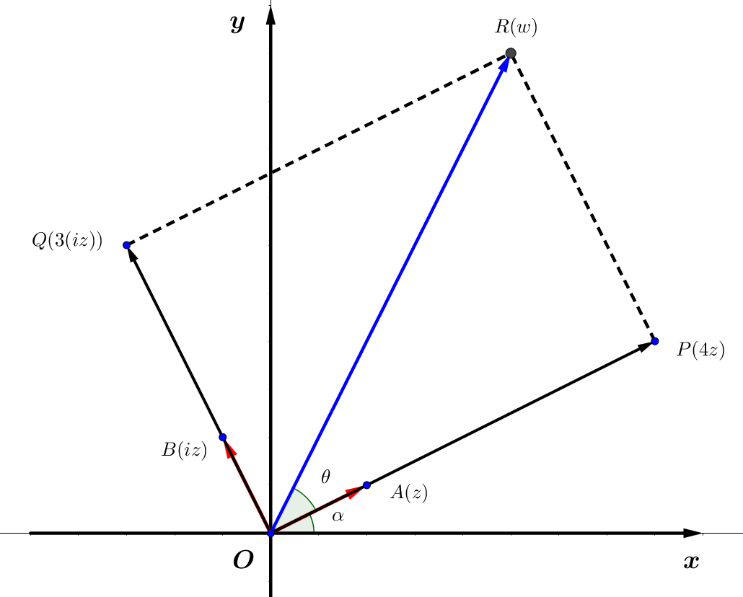
如右圖，設 $A(z)$、$B(iz)$，且令 $Arg(z)=\alpha$，$Arg(4+3i)=\theta$ ，根據分配律 $(4+3i)z=(4z)+3(iz)$，如圖， 描繪出 $P(4z)$、$Q(3(iz))$、$R(w)$， 因為 $z$ 繞原點逆時針旋轉 $90^{\circ}$ 可得 $iz$， 所以$\angle AOB=90^{\circ}$，故 $OPRQ$ 為矩形。 因為 $\overline{OP}=4|z|$， $\overline{OQ}=3|iz|=3|z|$，所以 $\frac{\overline{OP}}{\overline{OQ}}=\frac{4}{3}$。

• 考慮(4+3i)z的絕對值： $$ \begin{array}{rl} |(4+3i)z| & =\overline{OR}=\sqrt{\overline{OP}^2+\overline{OQ}^2} \\ & =\sqrt{(4|z|)^2+(3|z|)^2} \\ & =\sqrt{4^2+3^2}|z|=|4+3i||z|. \end{array} $$
• 考慮((4+3i)z)的輻角： 因為 $\frac{\overline{OP}}{\overline{OQ}}=\frac{4}{3}$，所以 $\angle POR= Arg(4+3i)=\theta$，故 $Arg((4+3i)z)= \alpha+\theta=Arg(z)+Arg(4+3i)$， 因此得到以下結果： $|(4+3i)z|=|4+3i||z|$， $(4+3i)z$ 的輻角可取為 $(4+3i)$ 與 $z$ 的輻角之和。